假期总该学点东西。对 SLAM 技术有一些兴趣，小开一个坑。

什么是 SLAM

S.L.A.M.全称为Simultaneous Localization and Mapping，是以定位和建图两大技术为目标的一个研究领域。目前主流的SLAM技术应用为激光SLAM(基于激光雷达)和视觉SLAM(基于单/双目摄像头)，实现上主要分为基于滤波（Filter-Based）的SLAM，和基于图优化（Graph-Based）的SLAM。

SLAM 的架构如下图所示。

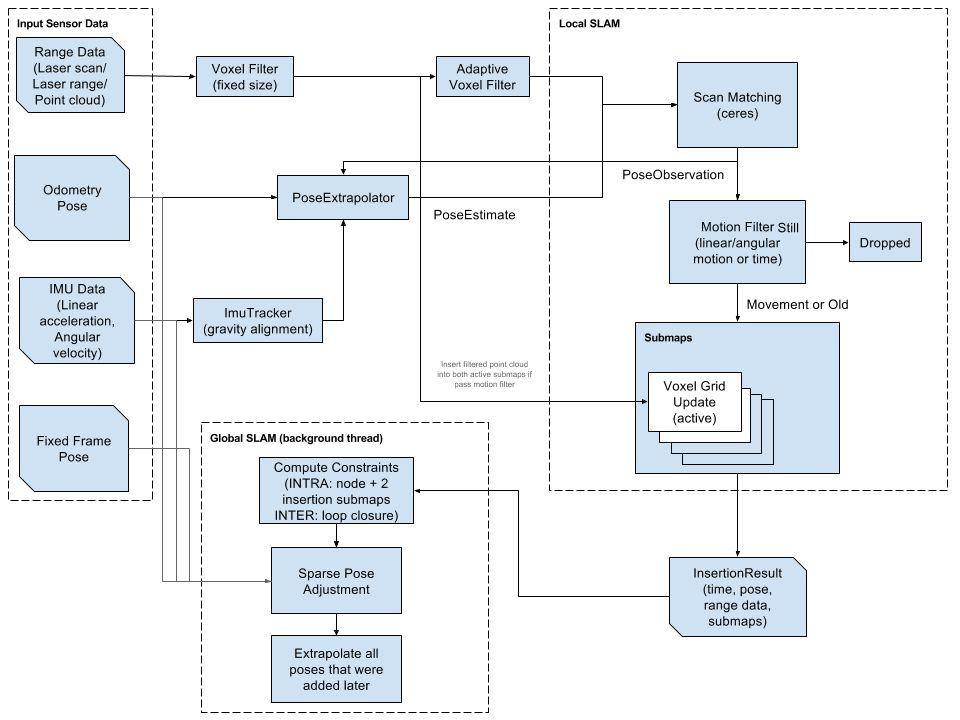
基于滤波的传感器融合算法方案

归结基于滤波的定位算法的核心技术，其实就是贝叶斯滤波或者其衍生算法。整体上的流程大抵都是基于上一时刻的状态量，通过控制量输入和运动方程的推演获取预测的状态量，再由相关传感器的观测对预测进行融合“补偿”。

滤波算法：卡尔曼滤波

今天预习复习一下机器人综合实践课程中介绍的卡尔曼滤波算法。

滤波器

在 DSP 中接触过滤波器。主要用于滤除信号中的噪声。以下面离散时间的低通滤波器为例：

$$ y_t=\alpha x_t + (1-\alpha)y_{t-1} $$

它的截止频率为 $f_c=\frac{\alpha}{(1-\alpha)2\pi \Delta t}$。其中 $\Delta t$是采样周期。任何频率大于 $f_c$ 的信号通过该滤波器都会得到极大的衰减，可以用于滤除高频噪声。

Kalman 滤波器则不同。它直接在时域中处理滤波问题，并且在线性系统下是最小方差估计。1960 年，时任美国宇航局加利福尼亚州 Ames Research Center（ARC）动力分析处主任的斯坦尼 • 施密特（Stanley F. Schmidt）正在阿波罗-11 号登月计划中主持导航项目。当年，宇宙飞船从陀螺仪、加速度计和雷达等传感器上获取的测量数据中充满了不确定性误差和随机噪声，严重地威胁着高速飞向月球并降落其岩石表面的宇宙飞船及宇航员的安全。因此他们必须从测量数据中把噪声滤掉，以便对飞船所处位置和运动速度作出非常精确的估算。经过多方认证和周密思考之后，施密特决定在阿波罗-11 号登月计划中采用 Kalman 滤波器，并成功让阿波罗-11 号在地球和月球之间飞了一个来回。

最小协方差估计与后验概率传递

Kalman 滤波器是对信号的最小方差估计，其实现手段是通过迭代的方式计算隐 Markov 模型中隐状态的后验分布的数学期望。

Kalman 滤波的数学原理

此处简化了推导，仅从噪声服从高斯分布的情况推导。事实上 Kalman 本人对于该滤波器的推导是基于 Hilbert 空间下的投影原理。

假设现有下列隐 Markov 模型：

$x_{t+1}=A_t x_t + Bu_t +w_t$ $y_t=C_tx_t+v_t$

其中 $x_t\in\mathbb R^n$ 为系统的状态；$y_t\in\mathbb R^p$ 为对系统的观测（或系统的输出），$w_t\sim \mathcal N(0,1)$ 为过程噪声，$v_t\sim\mathcal N(0,\Sigma_v)$ 为观测噪声；$w_t$ 和 $v_t$ 均为白噪声；初始状态的先验分布为 $x_1\sim\mathcal N(m_1,P_1)$。

依据上述假设，可知

$$ \begin{align*} p(x_{t+1}|x_t,u_t)=\mathcal N(A_tx_t+Bu_t,\Sigma_w) \\ p(y_t|x_t)=\mathcal N(C_tx_t,\Sigma_v) \end{align*} $$

以下有两个引理，证明略。

Lemma 1 若 $x\in\mathbb R^{d_x}\sim\mathcal N(m,p),y\in\mathbb R^{d_y}|x \sim \mathcal N(Hx+u,R)$，则 $x$ 和 $y$ 的联合分布服从

$$ \begin{bmatrix} x\\ y \end{bmatrix}\sim\mathcal N\left(\begin{bmatrix} m\\ Hm+u \end{bmatrix},\begin{bmatrix} P & PH^\top\\ HP & HPH^\top+R \end{bmatrix}\right) $$

Lemma 2 如果随机向量 $x\in\mathbb R^n$ 和 $y\in\mathbb R^m$ 服从以下联合高斯分布

$$ \begin{bmatrix} x\\ y \end{bmatrix}\sim\mathcal N\left(\begin{bmatrix} a\\ b \end{bmatrix},\begin{bmatrix} A & C\\ C^\top & B \end{bmatrix}\right) $$

则

$$ \begin{align*} x\sim \mathcal N(a,A),\quad y\sim\mathcal N(b,B) \\ x|y\sim\mathcal N(a+CB^{-1}(y-b),A-CB^{-1}C^\top)\\ y|x\sim\mathcal N(b+C^\top A^{-1}(x-a),B-C^\top A^{-1}C) \end{align*} $$

有了上述两个引理，我们可以在高斯噪声的假设下推导 Kalman 滤波器的迭代时。不妨假设 $x_t|u_{1:t-1},y_{1:t}\sim \mathcal N(\hat x_{t|t},P_{t|t})$。由引理 1 可得

$$ \begin{align*} p(x_{t+1},x_t|u_{1:t},y_{1:t})&=p(x_{t+1}|x_t,u_t)p(x_t|u_{1:t-1},y_{1:t})\sim\mathcal N(A_tx_t+Bu_t,\Sigma_w)\mathcal N(\hat x_{t|t},P_{t|t}) \\ &\sim\mathcal N\left( \begin{bmatrix} \hat x_{t|t} \\ A_tx_{t|t}+Bu_t \end{bmatrix},\begin{bmatrix} P_{t|t} & P_{t|t}A_t^\top \\ A_tP_{t|t} & A_tP_{t|t}A^\top+\Sigma_w \end{bmatrix}\right) \end{align*} $$

由引理 2 可得

$$ p(x_{t+1}|u_{1:t},y_{1:t})=\mathcal N(A_t\hat x_{t|t}+Bu_t, A_tP_{t|t}A^\top+\Sigma_w) $$

至此，我们得到了 Kalman 滤波器的前半部分 Prediction step:

$$ \begin{align*} \hat x_{t+1|t}=A_t\hat x_{t|t}+Bu_t \\ P_{t+1|t}=A_tP_{t|t}A^\top+\Sigma_w \end{align*} $$

另一方面，根据引理 1，有 $\begin{align*} p(x_{t+1},y_{t+1}|u_{1:t},y_{1:t}) &= p(y_{t+1}|x_{t+1})p(x_{t+1}|u_{1:t},y_{1:t}) \\ &\sim\mathcal N(C_tx_t,\Sigma_v)\mathcal N(\hat x_{t+1|t},P_{t+1|t}) \\ &=\mathcal N\left(\begin{bmatrix} \hat x_{t+1|t} \\ C\hat x_{t+1|t} \end{bmatrix},\begin{bmatrix} P_{t+1|t} & P_{t+1|t} C^\top \\ CP_{t+1|t} & CP_{t+1|t}C^\top+\Sigma_v \end{bmatrix}\right) \end{align*}$

根据引理 2，可进一步求得后验概率分布

$$ p(x_{t+1}|u_{1:t},y_{1:t+1})=\mathcal N(\hat x_{t+1|t+1},P_{t+1|t+1}) $$

其中，

$$ \begin{align*} &\hat x_{t+1|t+1}=\hat x_{t+1|t}+P_{t+1|t} C^\top(CP_{t+1|t}C^\top+\Sigma_v)^{-1} (y_{t+1}-C\hat x_{t+1|t}) \\ &P_{t+1|t+1}=P_{t+1|t}-P_{t+1|t}C^\top(CP_{t+1|t}C^\top+\Sigma_v)^{-1} C(P_{t+1|t}) \end{align*} $$

此即 Kalman 滤波器的后半部分 Correction (Update) Step。

此，我们得到了 Kalman 滤波器的后半部分——Correction （Update）Step。Kalman 滤波器通过 Prediction step 和 Correction step 交替迭代，成功地通过 $p(x_t | u_{1:t−1}, y_{1:t})$ 来计算 $p(x_{t+1} | u_{1:t} , y_{1:t+1})$。值得注意的是，该算法需要一个初始分布 $p(x_1)$，用于求 $p(x_1 | y_1)$，所以我们需要指定 $x_1$ 的先验分布 $x_1\sim \mathcal N (m_1, P_1)$。